삽입 정렬
위키백과 ― 우리 모두의 백과사전.
삽입 정렬은 자료 배열의 모든 요소를 앞에서부터 차례대로 이미 정렬된 배열 부분과 비교하여, 자신의 위치를 찾아 삽입하므로써 정렬을 완성하는 알고리즘이다. 배열이 길어질수록 효율이 떨어지지만, 구현이 간단하다는 장점이 있다.
선택 정렬이나 거품 정렬과 같은 같은 O(n2) 알고리즘에 비교하여 빠르며, 안정 정렬이고 in-place 알고리즘이다.
목차[숨기기] |
[편집] 예제
다음의 주어진 리스트의 삽입정렬은 다음과같다.
31 25 12 22 11 // 가장 앞의 값 31부터 비교를 시작한다. 11 25 12 22 31 // 31은 최대값이므로 맨뒤에 위치 11 12 25 22 31 // 다음값 25는 12보다 크므로 교환 11 12 22 25 31 // 값 25는 22크고 31작으므로 값22와 교환
[편집] 소스코드
[편집] C example
void insertion_sort ( int *data, int n ) { int i, j, remember; for ( i = 1; i < n; i++ ) { remember = data[(j=i)]; while ( --j >= 0 && remember < data[j] ) data[j+1] = data[j]; data[j+1] = remember; } }
/* 아래는 정렬되는 자료가 단순 데이터일 경우에 memcpy()로 자료를 밀어내는 예제 */ /* memcpy 는 자료를 당겨야하므로 비교를 역순으로 수행한다. */ /* memcpy 를 이용하면 위의 코드보다 25~30% 가량 빠르게 처리된다. */ void insertion_sort ( int *data, int n ) { int i = n-2, j, remember; while ( i-- > 0 ) { remember = data[(j=i)]; while ( ++j < n && remember > data[j] ); if ( --j == i ) continue; memcpy ( data+i, data+i+1, sizeof(*data) * (j-i) ); data[j] = remember; } }
[편집] C++ example
void insert(const Element e,Element *list,int i) { while(e.getKey()<list[i].getKey()) { list[i+1]=list[i] i--; } list[i+1]=e; }
[편집] JAVA example
/* * insertion Sort의 오름차순 정렬은 배열을 순차적으로(1~n) 까지 검색함. * arr[] 는 int[]라고 가정함. */ void insertionSort(int[] arr) { for(int index = 1 ; index < arr.length ; i++){ int temp = arr[index]; int aux = index - 1; while( (aux >= 0) && ( arr[aux] > temp) ) { arr[aux+1] = arr[aux]; aux--; } index[aux + 1] = temp; }
[편집] Objective Caml example
let rec isort = function | [] -> [] | h::t -> insert h (isort t) and insert a = function | [] -> [a] | h::t when a<h -> [a] @ (h::t) | h::t -> [h] @ (insert a t);;
[편집] 복잡도
최악의 경우 i+1번의 비교를 하게되고 이때의 시간복잡도는 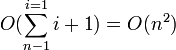 이 된다.
이 된다.
'Algorithm' 카테고리의 다른 글
| HDLC 프로토콜 (0) | 2008.08.26 |
|---|---|
| 셀정렬 (1) | 2008.08.23 |
| 스케쥴링 (0) | 2008.08.19 |
| 선점,비선점 스케쥴링 (1) | 2008.08.19 |
| 병행프로세스와 상호배제 (0) | 2008.08.19 |





