전자서명
1 내용
가) 개인 키와 함께 생성된 메시지 다이제스트
나) 서명
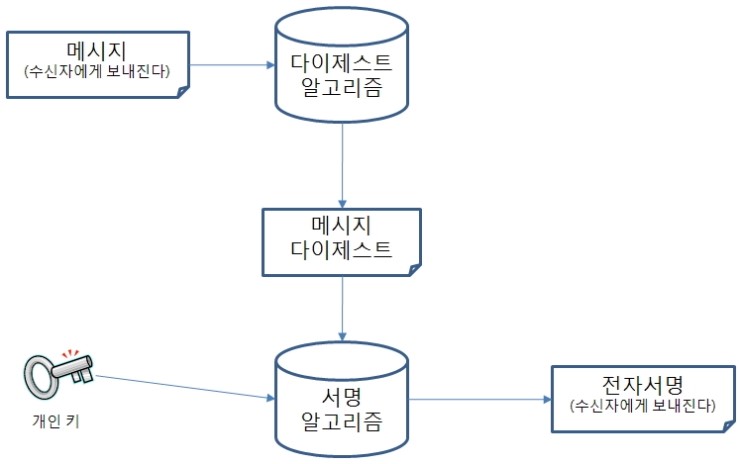
다) 서명 검증
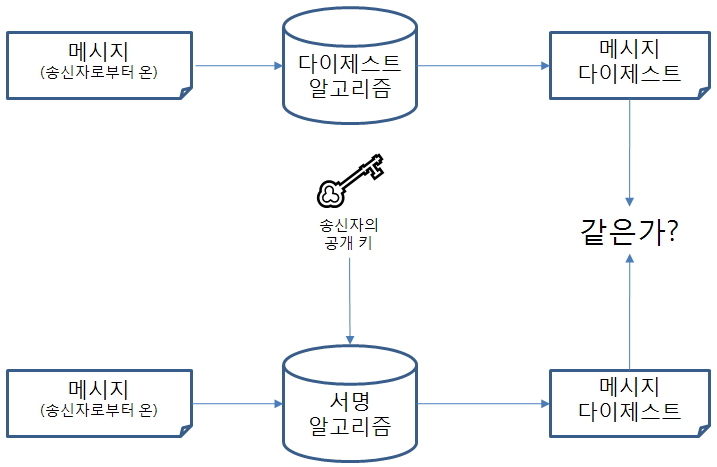
2 목적
가) 무결성
① 데이터에 대해서 바뀌지 않았다는 것을 증명
② 데이터와 메시지 다이제스트 두 개를 다 바꿀 수 있음
③ 다이제스트를 개인키로 서명하면 이것은 불가능해 짐
나) 인증
① 개인 키의 소유자만이 데이터에 서명할 수 있음
② 키가 안전하다면 사용자가 실제로 서명했다는 것을 확신할 수 있음
3 활용
가) 계약서에 서명
① 1999년 7월부터 ‘전자서명법’이 발효됨
② 기존의 일반 종이문서에 사용되는 인감이나 서명과 같은 법적 효력을 갖게 됨
나) 이메일 서명
① S/MIME나 PGP를 사용해서 개인 키로 이메일을 서명할 수 있음
다) 타임서버 생성
① 타임 스탬프는 데이터에 시간과 함께 서명해서 어떤 특정 시간에 정보가 존재했는지를 증명
라) 서버 승인
① 요청에 서명을 하면 사용자가 서버가 특정한 개인 키를 가졌는지 확인 가능
4 RSA vs. DSA
가) RSA
① 서명을 검증하는데 빠름
나) DSA(Digital Signature Algorithm)
① RSA에서 서명하는 것과 비슷하지만 암호화 기능은 없음
② 서명을 만드는데 빠름
5 자바의 전자 서명
가) java.security.Signature
① getInstance() : 알고리즘 이름을 인자로 해서 객체의 인스턴스 획득
② initSign() : 개인 키를 인자로 서명
③ initVerify() : 공개 키를 인자로 검증
④ update() : 데이터를 전달하여 서명/검증을 수행
⑤ sign() : 전자서명을 반환
⑥ verify() : 전자서명의 유효성을 반환
6 간단한 전자서명 예제
|
import java.security.KeyPair; import java.security.KeyPairGenerator; import java.security.Signature; import java.security.SignatureException;
import com.Ostermiller.util.Base64;
public class SignatureExample {
public static void main(String[] args) throws Exception{ //RSA 키 쌍 생성 System.out.println("RSA 키 쌍 생성..."); KeyPairGenerator kpg = KeyPairGenerator.getInstance("RSA"); kpg.initialize(1024); KeyPair keyPair = kpg.genKeyPair(); System.out.println("RSA 키 쌍 생성 완료");
// 서명할 데이터 byte[] data = "i love you.".getBytes("UTF-8");
// 서명을 위해 Signatrue 객체 생성 및 개인 키로 초기화 Signature sig = Signature.getInstance("MD5WithRSA"); sig.initSign(keyPair.getPrivate()); sig.update(data); // 실제 서명 byte[] signaturedBytes = sig.sign(); System.out.println("전자서명된 데이타 : " + Base64.encode(signaturedBytes));
// 전자서명 검증 sig.initVerify(keyPair.getPublic()); sig.update(data); boolean verified = false; try { verified = sig.verify(signaturedBytes); } catch (SignatureException e) { verified = false; System.out.println("전자서명 형식에 문제가 발생하였습니다."); e.printStackTrace(); }
if(verified) System.out.println("전자서명 검증 성공"); else System.out.println("전자서명 검증 실패");
}
} |
7 전자 서명의 한계
가) 검증을 위해서 공개 키가 필요
나) 공개 키의 소유자를 확신하기가 힘듬
다) 전자 인증서로 문제 해결




