▶ 다단계 색인의 가장 대표적인 색인 구조 B- 트리와 B+- 트리
B- 트리
B+- 트리
특 징
o 균형 m-원 탐색 트리
o 차수 m인 B-트리의 특성
- 루트와 리프를 제외한 노드의 서브트리 수 ≥ 2
* [m/2] ≤ 개수 ≤ m
- 모든 리프는 같은 레벨
- 키 값의 수
* 리프 : [m/2] -1 ~ (m-1)
* 리프가 아닌 노드 : 서브트리수 - 1
- 한 노드 내의 키값 : 오름차순
o 노드 구조
- Ki→ (Ki,Ai): 데이타 화일의 주소(Ai)
o 인덱스 세트 (index set)
- 내부 노드
- 리프에 있는 키들에 대한 경로 제공
- 직접처리 지원
o 순차 세트 (sequence set)
- 리프 노드
- 모든 키 값들을 포함
- 순차 세트는 순차적으로 연결
→ 순차처리 지원
- 내부 노드와 다른 구조
연
산
탐색
o 직접 탐색 : 키 값에 의존한 분기
- 순차 탐색 : 중위 순회
- 삽입, 삭제 : 트리의 균형 유지
- 분할 높이 증가
- 합병 높이 감소
- B+-트리의 인덱스 셀 = m-원 탐색 트리
- 리프에서 검색
삽입
리프노드
- 빈 공간이 있는 경우: 순 삽입
- 오버플로
* 두 노드로 분열(split)
* [m/2] 째의 키 값 → 부모노드
* 나머지는 반씩 나눔 (왼쪽, 오른쪽 서브트리)
- B-트리와 유사
- 오버플로우 (분열)
→ 부모 노드, 분열노드 모두에 키 값 존재
삭제
- 리프노드
- 삭제키가 리프가 아닌 노드에 존재
* 후행키 값과 자리교환(후행키-항상 리프에)
* 리프노드에서 삭제
- 언더플로 : 키수 < m/2�-1
* 재분배 (redistribution)
- 최소키 수 이상을 포함한 형제노드에서 이동
(형제노드의 키 → 부모노드 → 언더플로노드)
*합병 (merge)
- 재분배 불가능시 이용
(형제노드 + 부모노드의 키 + 언더플로노드)
리프에서만 삭제 (재분배, 합병 필요 없는 경우)
- 재분배: 인덱스 키 값 변화, 트리구조 유지
- 합병 : 인덱스의 키 값도 삭제
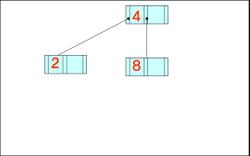
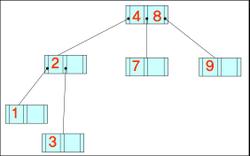
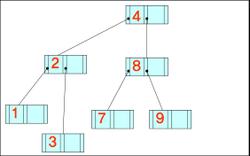
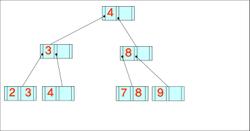
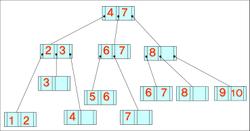
- 데이터가 왼쪽부터 차례대로 입력될 때 구축된 B-트리와 B+-트리의 최종적인 형태(차수는 3)
4, 8, 2, 3, 9, 7, 1, 6, 10, 5
B- 트리
B+- 트리
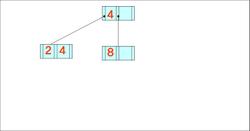
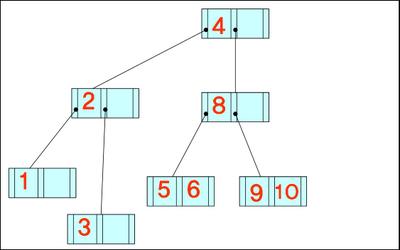
+ 위의 구축한 트리에서 키 값 7이 삭제된 후 모습
B-트리
B+- 트리
'Algorithm' 카테고리의 다른 글
| RISC 기본원리 (0) | 2008.08.19 |
|---|---|
| deadlock 4가지 (0) | 2008.08.01 |
| CPU scheduling (0) | 2008.08.01 |
| 스케쥴링 기법 (0) | 2008.08.01 |
| banker's algorithm (1) | 2008.08.01 |